Fixing My Stairs Using Mathematics

The Problem

I am a VERY amateur carpenter, but I do love to build things out of wood. One particular specialty area of carpentry that I admire is stair building. I consider stair building (along with roof cutting) to be the brain surgery of carpentry. While occasionally stairs are works of art, they always must be safe and functional. Quite often, I see stairs where the height of either the bottom step or top step is not the same as the other stairs. This is nearly always because the flooring on the bottom or top floors has changed since the stairs were built. Unfortunately, I recently faced this same situation.

I live in a cold climate and my house has a basement. In order to make the basement livable in the winter, I hired a contractor to build an insulated floor, which is very thick compared with the original carpeting. Unfortunately, the additional lower floor height made the bottom step of my basement stairs very short. This created a safety issue and would be an issue if I were to try and sell the house. The city building inspector noticed the issue, but decided not to force the contractor to fix it. Given that option, the contractor left it short.

A few years after my basement floor was insulated, my wife and I decided to put a wood floor in the basement and re-carpet the stairs. Because the stair framework was exposed, this remodeling gave us an opportunity to equalize all the riser heights with minimal hassle. Unfortunately, we decided to equalize the riser heights the night before the carpet was due to go in. I contacted a carpenter for advice who said that I should just cut a new set of "stringers," which are the wooden supports that the treads sit on. This would not work, however, because the hour was late and I had neither the lumber nor the equipment to cut the stringers. After thinking about it a bit, the easiest solution was to use shims under each tread to set the unit rise for each tread. This is where a little bit of math came into play.

A Few Definitions

There are many special terms associated with the building of stairs. For this discussion, there are just a few terms that need to be defined. I have illustrated these terms in the following figure.

Illustration of a Few Stairway Terms

The situation that I faced was that my new insulated lower floor was now higher by 2.25 inches than when the stairs were originally built. The insulated floor was built using 2x4s (i.e. 1.5 inches thick) glued to my basement concrete surface to support a 0.75 inch thick floor surface made of plywood. Styrofoam insulation was placed between the plywood and the basement concrete surface. This was one of the best improvements I have made to my house, but it did raise my floor. The figure below illustrates the situation, along with some of the critical dimensions. Note that my actual stairs has many more treads than the four shown in this drawing but the drawing illustrates the problem just fine.

My Short Bottom Step Makes My Stairway Unsafe

The Fix

Let R be the unit rise before the floor height change, R' be the unit rise after the floor height change, T be the total rise before the floor height change, T' be the total rise after the floor height change, and N be the number of stairs. The unit rises before and after the floor height change are computed as follows.

${R} = \frac{T}{N}, {R'} = \frac{T'}{N}$

Our objective here is to derive an expression for the thickness of each shim. In order to easily identify each individual shim height, we can assign a number to each stair tread — assign the bottom tread the number 1 and increment the number for each tread going up (top tread is actually the top finished floor and is assigned N). Each tread will be assigned a specific shim thickness. Let $\tau_i$ be the shim thickness for the ith tread. For the sake of simplicity, we can define $\tau_0$ as the height increment of the newly finished lower floor height from the original floor height.

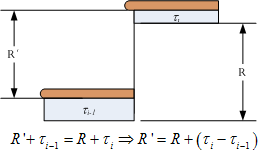
The following figure is useful in understanding the derivation of an expression for the shim thickness. It shows the relationship between the rise values before and after the shims.

Detail Drawing of An Individual Step

Using the figure above, we can see that the following relationship exists between R, R', $\tau_{i}$ , and $\tau _{i-1}$ .

$R' + {\tau _{i - 1}} = R + \tau {}_i \Rightarrow R' = R + \left( {\tau {}_i - {\tau _{i - 1}}} \right)$

Since each stair must be the same height and our overall stair height is shorter by $\tau_0$ , the difference between the old and new stair heights must be ${}^{{{\tau }_{0}}}\!\!\diagup\!\!{}_{N}\;$ . Given this difference, we can derive a relationship between the heights of the individual shims as follows.

$R - R' = - \frac{{{\tau _0}}}{N} = \left( {\tau {}_i - {\tau _{i - 1}}} \right) \Rightarrow {\tau _i} = {\tau _{i - 1}} - \frac{{{\tau _0}}}{N}$

This expression means that a shim's height is always $\frac{\tau _0}{N}$ smaller than the shim on the next lower step.

Let's compute a few shim heights to illustrate the situation.

${\tau _1} = {\tau _0} - \frac{{{\tau _0}}}{N} = {\tau _0} \cdot \frac{{N - 1}}{N}$

${\tau _2} = {\tau _1} - \frac{{{\tau _0}}}{N} = {\tau _0} \cdot \frac{{N - 2}}{N}$

$\vdots$

${\tau _{N - 1}} = {\tau _0} - \frac{{\left( {N - 1} \right) \cdot {\tau _0}}}{N} = {\tau _0} \cdot \frac{1}{N}$

${\tau _N} = {\tau _0} - \frac{{\left( N \right) \cdot {\tau _0}}}{N} = 0$

There is a pattern here and the thickness of the ith shim is given by the following equation.

${\tau _i} = {\tau _0} \cdot \frac{{N - i}}{N}$

We now have all the information we need to cut the shims and fix the stairs. Here is what the stairs looked like after the shimming was completed.

Shimming Equalizes All Unit Rises

My basement steps have been working without problems now for years. The unit rise of each step is exactly the same. All it ended up costing me was some scrap lumber, a little glue, and a little time to derive a solution. What more could I ask for?

Some Practical Issues

IRC Requirements

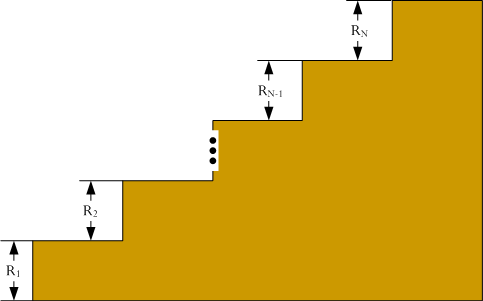
The main requirement of concern in this situation is the IRC constraint on the allowed variation in riser heights. To understand this requirement, consider the flight of stairs illustrated in the following figure.

Illustration of Riser Height Deviations

The IRC requires that the following requirement be met.

$\max \left( {{R_1},{R_2}, \cdots ,{R_{N}}} \right) - \min \left( {{R_1},{R_2}, \cdots ,{R_{N}}} \right)\; \leqslant \;\frac{3}{8}{\text{ inch}}$

For more information on the IRC stairway requirement, see [1].

Dealing with Thin Shims

When I did my stairs, I worked too hard to make thin shims. If I had it to do over today, I would not have made any shims thinner than 1/8 inch. I would simply ensure that I met the IRC requirement that limits the maximum difference between riser heights to 3/8 inch. Making and installing thin strips is difficult because they are so fragile that they are not worth the effort.

A Reference with a Similar Approach

I did find one reference ([2]) that uses a similar method for fixing a flight of stairs, but the description is is not quite as detailed as presented here.

References

[1] "Visual Interpretation of the International Residential Code:2006 Stair Building Code", Stairway Manufacturers Association, 2006. Link
[2] B. Abernathy, "Q&A: Your Questions—Pro Answers: Fixing Rough Framed Stairs," Fine Homebuilding Magazine, Issue 168, pp. 106, Jan 2005. Link

Save

13 Responses to Fixing My Stairs Using Mathematics

Nora says:

16-October-2013 at 8:55 pm

I am an architect who plans and details custom stairs regularly. My biggest concern is how substantial are these shims? They need to support the weight of the new tread and those walking on it. They should be solid so the new tread does not span between shims. Also, you are adding a substantial amount of weight to the existing stringers with the new built up treads and risers, so you will need to be careful that the existing stringers and their anchors are strong enough to support the additional dead load added.
Not a very elegant solution, but it should work as long as precautions are taken.
- mathscinotes says:
  
  16-October-2013 at 9:54 pm
  
  You are correct that you need to ensure the shims are as solid as the treads. That is one of the reasons that I mentioned at the end of the document that you should not cut them too thin. In my case, I made the thick shims out of 2x stock. The thinner shims were from solid sheet stock, also the same length as the tread. I did not go into detail in the article, but I also added additional bearing area where the stringers had shims -- not all treads had stringers because they would have been too thin.
  
  As far as mass, I doubt I added 40 lbs.
  
  mathscinotes
Dale says:

28-September-2014 at 6:48 pm

Hi Math',
Thanks for the formula and explanation.
Nora above seems to think you altered the risers as well as the treads - but I don't see that anywhere.
- mathscinotes says:
  
  28-September-2014 at 10:59 pm
  
  Thanks for the comment. I just shimmed the tread. I am not sure what the issue with the riser would be. I just came down those stairs. Everything still working and looking good.
  
  mathscinotes
Subhendu Chakraborty says:

29-June-2016 at 2:12 pm

That is a cool equation. I suppose that will work for adjusting the other direction. Like in my case the the first stair will become higher than the rest. I want to add 1" oak stair tread on top of the bare rough builders treads. Currently it has carpet all the way including the upstairs floor and down stairs. The heights of all steps are 7.5" without any carpet. If I keep adding 1" tread, the first step becomes 1 inch higher than the rest. So according to your formula I should take off from each tread certain amount, Correct?
Like take 0.93 from the first tread, 0.875" from the 2nd and so on? I have 16 steps including the landing on 2nd floor. If wrong, please let me know.
- mathscinotes says:
  
  21-July-2016 at 11:36 am
  
  The shims are trimmed to a height specific for each step. In theory, you would have to trim a shim for each step. In practice, the code requires that each step be equal within an 1/8 inch. So you would not need to make a shim thinner than 1/8 inch, assuming the steps are all the same height initially.
  
  mathscinotes
Subhendu Chakraborty says:

29-June-2016 at 2:14 pm

It is harder to trim off than adding shims. Is there any other ways of doing this? Many regular carpenters told that they will just adjust the first step by cutting.. Which does not seem right.
- mathscinotes says:
  
  21-July-2016 at 11:39 am
  
  I cut my shims on a table saw. I had not thought about adding small shims together to make a bigger shim. Multiple small shims probably would work. I personally would cut mine to size to ensure that the shims were strong.
  
  mathscinotes
Pingback: Layout Formula for a Balustrade | Math Encounters Blog
Subhendu Chakraborty says:

21-July-2016 at 12:00 pm

Thanks for your reply. My situation is just opposite of your situation. My finished first floor is lower than it should be to make all the other steps equal height. Like if all the steps currently are 7.5" height, by adding 1 inch tread on top of builders existing rough tread, it makes all steps still 7.5" height except the first step from first floor will be 1 inch higher than the rest, since there is no added tread on the first floor. That is not acceptable, so I have to trim off the stair heights to adjust, instead of shimming. Right?

I think your formula still will work but in the negative direction??
- mathscinotes says:
  
  21-July-2016 at 5:07 pm
  
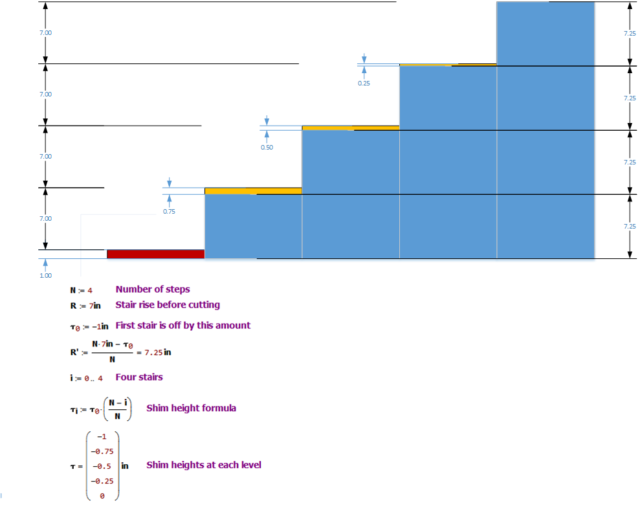
  The formula works for negative directions. Here is an example using a stairs with 7 inch risers and the bottom step is lower by 1 inch. The new stairs will have 7.25 inch risers. Each riser needs to be cut down. The following figure illustrates this case and the calculations.
Pingback: Shimming and Trimming Stairs to Equalize the Risers | Math Encounters Blog
Subhendu Chakraborty says:

21-October-2016 at 3:41 pm

Thank you.
I have another question. If the stair treads are out of code by the minimum depth (should be 10" from nosing to next step's nosing) how to fix easily. Instead of 10" depth for all of the 15 steps, a stupid professional carpenter made them 9.5" instead. Is there a mathematical trick to quick-fix?
Also the nosing projections are already at max (1-1/4" allowed by code) and can only make it less but not more.

Thank you