Magic Number Analysis – Converting Spectral Width to Sigma

Posted on 12-October-2010 by mathscinotes

Introduction

Engineering seems to have a lot of "magic numbers" – numbers used in equations with no explanations of where they come from. I REALLY do not like magic numbers because years from now some other engineer will be staring at this equation and asking the same question I just did – "Where did this number come from?" I encountered one this morning and I thought it would be worthwhile to document where it came from.

The magic number is "6.07." I saw a web site that recommended dividing the spectral width of a laser by 6.07 when performing some basic calculations. This blog describes where the number comes from.

Analysis

Side-Mode Suppression Ratio and Spectral Width Definitions

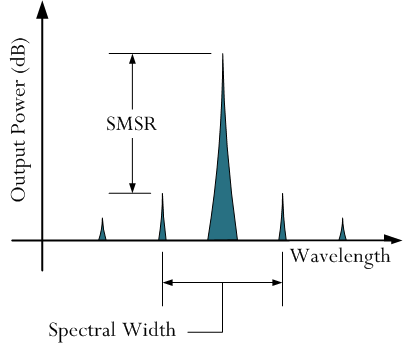
I was looking at at laser specification and it contained two numbers of interest: Side-Mode Suppression Ratio (SMSR) and spectral width. SMSR is a measure of the wavelength purity of a laser's output. It is defined as the ratio of the power in the dominant mode to the power in the strongest side mode. Spectral width (\Delta\lambda is the wavelength range between the points at the SMSR level. Figure 1 illustrates how the measurement is made.

Figure 1: Illustration of SMSR and Spectral Width.

Figure 1: Illustration of SMSR and Spectral Width.

Figure 2 shows the spectrum for a laser with a 45 dB SMSR (Source: Gipo).

Figure 2: Wavelength Spectrum of an Actual Laser (Source: Gipo).

Figure 2: Wavelength Spectrum of an Actual Laser.

Laser Spectral Modeling

We often model the output spectrum of a laser using the normal curve, which makes sense when there is a main lobe and minimal side-lobe structure, like Figure 2. A normal curve is characterized by three numbers:

  • peak value (A)
  • mean wavelength (\mu)
  • standard deviation (\sigma)

The SMSR is used to estimated the standard deviation of the normal curve that best models the laser spectrum.

Spectral Width

There are two common ways to measure the spectral width.

  • Full-Width Half Maximum (FWHM – Generally used only with FP lasers)
    This approach measures the pulse width at the 50% power points.
  • Side Lobe Suppression Ratio (SMSR – Generally used only with DFB lasers)
    This approach measured the pulse width from the points that are 20 dB down.

These approaches are designed to make measurement simple, but they do not directly give you a standard deviation. A conversion is required. Since I am most interested DFB lasers, I will focus on converting an SMSR-based \Delta\lambda measurement to a standard deviation.

- 20 = 10\log \left( {\exp \left( {\frac{{\lambda _{ - 20{\text{ dB}}}^2}}{{2 \cdot \sigma _\lambda ^2}}} \right)} \right)

{10^{ - 2}} = \exp \left( {\frac{{\lambda _{ - 20{\text{ dB}}}^2}}{{2 \cdot \sigma _\lambda ^2}}} \right)

\ln \left( {{{10}^{ - 2}}} \right) = \frac{{\lambda _{ - 20{\text{ dB}}}^2}}{{2 \cdot \sigma _\lambda ^2}}

\frac{{{\lambda _{ - 20{\text{ dB}}}}}}{{{\sigma _\lambda }}} = \pm \sqrt {2 \cdot \ln \left( {{{10}^{ - 2}}} \right)} = \pm 3.035

where \lambda_{-20 dB} is one of the two wavelengths where the spectral amplitude is down -20 dB from the peak. We define the \Delta\lambda as the difference between the two \lambda_{-20 dB} values. Figure 3 illustrates the measurement.

Figure 3: Illustration of Critical Normal Curve Parameters.

Figure 3: Illustration of Critical Normal Curve Parameters.

So to convert \Delta\lambda to \sigma_\lambda, simply divide the \Delta\lambda value by 6.07 as shown below.

{\sigma _\lambda } = \frac{\Delta\lambda}{6.07}

Conclusion

The post shows that the standard deviation of a laser's spectrum can be computed by dividing that laser's spectral width (i.e. the wavelength range between points 20 dB down from a laser's spectral peak) by 6.07.

This entry was posted in Fiber Optics and tagged , , , . Bookmark the permalink.

4 Responses to Magic Number Analysis – Converting Spectral Width to Sigma

  1. Joel says:
    1-November-2010 at 6:10 pm

    Magic numbers are only magic to those who don't know the source. We all know that pi is 3.14159. Most know it is the ratio of a circle's circumference to its diameter. Few know how to take that and generate a real number.

    The people who toss around 6.07 knew the source of the value at some point. Now they just use it because they have been for many years.

    • mathscinotes says:
      1-November-2010 at 7:08 pm

      You are correct. This particular magic number came up because we are getting ready for some new product designs and some of the part vendors have changed how they specify the performance of their parts. So where we used to be able to use the same magic number for each part, we now must look at how each vendor defined this parameter and use a specific magic number for their definition. I have decided that I need to write down the background on these numbers as I encounter them. It turns out there are about 4 ways to specify this parameter, hence 4 magic numbers. I will document them as I go through them.

  2. Muhammed Ali says:
    21-May-2012 at 12:30 am

    Great definition and graph for SMSR. Thank you!

  3. Pingback: Chromatic Dispersion with 10 Gigabit Optical Transports | Math Encounters Blog

Comments are closed.