Introduction
An engineer came by my cube and asked me a question about a part we use in one of our older designs. This clever little device is made by Maxim and is called the 3660. This chip is used to convert an optical version of a television signal into its electronic counterpart. Video service providers transport their video signals around optically, but must convert the optical signal to its electronic form for use by standard televisions. Because optical signal strength decreases with the distance it must travel, we need a way to compensate for the loss of signal level. TV watchers like to receive signals with a constant signal level to ensure that they do not have to watch poor quality images. The service providers also like this feature because it means that they can service customers over a wide range of distances with no degradation in signal quality, simplifying their system designs. Ideally, we would use a receiver that would convert our optical signal to an electrical signal that has a constant level regardless of the optical input level.
What the design engineer needs is an amplifier whose gain will increase when the input voltage decreases. This feature is usually referred to as Automatic Gain Control (AGC). The engineer who came to my cube had noticed something odd in how the AGC feature of this circuit works compared to other amplifiers with AGC – the 3660 has a hyperbolic AGC characteristic. This is where my story begins.
Background
AGC common in electronics. Normally, the gain of AGC amplifier varies linearly or logarithmically with the voltage placed on one of the chip's pins. Figure 1 shows an example of a typical linear variable gain amplifier characteristic. The voltage used for AGC is referred to as VAGC.

Figure 1: Typical Variable Gain Amplifier Characteristic
The gain of the amplifier increases linearly with the voltage on the AGC pin.
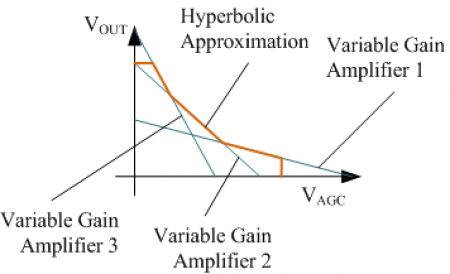
The engineer at my cube had noticed that the Maxim 3660 does not have a linear or logarithmic gain characteristic – it has a hyperbolic characteristic (see Figure 2).
What is a hyperbolic curve doing in there? When I first saw the part, I had the same question. The 3660 was designed by Javier Sanchez, an analog guru whose designs are absolutely first-rate. He had a good reason to design it this way.
Analysis
Design Rationale
The output voltage of the 3660 is described by Equation 1. In Equation 1, I am ignoring the clipping that occurs at both high and low AGC voltages. We never operate our systems in those areas of the AGC curve, so we can ignore them.
| Eq. 1 |
where
- VIN is the input voltage to the amplifier.
- VOUT is the output voltage from the amplifier.
- VAGC is the gain control voltage.
- K is a constant term.
Equation 1 shows us that the gain of the amplifier indeed varies hyperbolically with VAGC. A close look at Equation 1 also shows us what we must do to maintain a constant output from this amplifier. What if we make , where K0 is a constant? The result is shown in Equation 2.
| Eq. 2 | |
Equation 2 shows that the 3660 will generate a constant output if we make VAGC proportional to the input voltage. It turns out that this is very easy to do. In our actual implementation, we set VAGC to a value that is proportional to the DC level of the input signal (the AC portion of the signal is the actual information). The proportionality (K0) is set so that the constant output level is the value you desire.
This approach was used in an early version of our products and we have shipped hundreds of thousands of these units to happy TV watchers.
How Did Javi Do It?
Electronic designs routinely work with circuit parameters that vary linearly or exponentially, which makes generating these curves a breeze. However, generating a hyperbola does not come easily. When an integrated circuit designer approaches a problem, he looks reuse existing designs as much as possible to minimize his design effort. In the case of the 3660, Javi used three copies of an existing linear variable gain amplifier design. Using standard techniques, he pieced their characteristics together as shown in Figure 3.
While the basic concept shown here is simple, there are numerous details that must be dealt with to ensure that the amplifiers turn on and off at the proper times. I will not cover these details in this post. Just understand that there is quite a bit of work involved in turning any good idea into a credible piece of silicon. The piecewise linear approximation to a hyperbolic curve worked just fine for a real world application and it was simple for the chip's end users to apply.
Conclusion
The 3660 variable gain amplifier design is a good example of a design engineer understanding the problem he was solving and working to solve the problem in the most direct way possible. This design ended up providing high performance at very low cost. I really can't ask any more than that.


Hi,
I am Javier Sanchez, are you MB?
I am really glad to see a customer appreciating one of my kids. We (myself and MW) had a lot of fun with these analog TIAs.
Keep working on this blog, I read it from time to time. The real problem with the use of the math language is how to translate the intuition to equations and symbols. Once you get that working after years of training and practice you find yourself doing more and more BIG math. You can always study BIG maths but your blog is teaching us how to start with simple things and how useful is to be fluent with the new language.
Regards
Javi
Hi Javier,
Yes, I am MB. I have always admired your work -- I consider it math chiseled in silicon. I hope all is well. Things are good here.
Mathscinotes