Battery Life Dissipated Under Varying Temperature Conditions

Introduction

I am not getting any younger. As I age, I have come to realize that certain activities age me faster than others. For example, I have no doubt that sitting in meetings for hours every day has deleterious effects on my health. In the case of batteries, higher temperatures age batteries faster than lower temperatures. This post works through two examples in detail to illustrate how to model the rate of battery aging under varying temperature conditions.

I am usually asked about battery life aging with respect to two types of temperature profiles: (1) a battery operating at a few discrete temperatures and (2) a battery operating at a continuously varying temperatures. The analysis methodology is the same in both cases. I will provide examples of both cases.

Background

General Battery Aging Model

I have written extensively about battery aging models in other posts (e.g. here). In those posts, I assumed that the battery temperature was constant. I recently had a customer request that I analyze the impact of varying temperature on a battery's life. This problem was interesting enough that I thought it was worth documenting here.

I will be using the model of IEEE 450-2002 for this post. For those of you in need of a review, take a look here. For another reference, McCluer's paper also uses the same approach.

Computational Model

Every lead-acid battery vendor specifies the expected lifetime of their battery. Most of these batteries have 3 to 5 year lifetimes at 25 °C. However, some batteries are rated to have lives as long as 12 years at 25 °C. In this post, I will compute a conversion factor that will adjust the vendor's specified lifetime for a non-constant temperature profile.

I have done these calculations a couple of different ways. I have estimated battery life using two approaches:

Equivalent 25 °C Time

Express battery life in equivalent 25 °C days. I do not like this approach myself, but some customers will tell me that their operational model requires an 8 year life for a specific temperature profile. They then want to compute an equivalent lifetime at 25 °C, which is how the battery manufacturer's specify their products.

Actual Time

Express battery life in actual days using the customer's temperature profile. I prefer this approach because I generally know the battery that is going to be used and I want to estimate this batteries life under the customers temperature profile.

My approach is simple:

• Determine the customers temperature profile

  Sometimes the customers gives you their profile and sometimes they tell you that they are doing a deployment in a certain community, like Phoenix (a case that I studied for this very reason).

• Express the customer's temperature profile in terms of temperature versus percentage of time at that temperature.

  We are going to be computing a weighted average and we need to know the percentage of time the battery spends at each temperature.

• Compute a conversion factor between 25 °C time and customer profile time.

  Knowing the equivalence between the different temperature profiles (e.g. customer profile versus constant 25 °C), we can generate terms of equivalent 25 °C days or actual days.

Equation 1 shows how I plan to use the conversion factor to adjust the battery's rated lifetime.

Eq. 1

where

• K is the nominal lifetime conversion factor [unitless]
• T_{Life_At_25°C} is the battery manufacturer's rated lifetime for the battery at a reference temperature (usually 25 °C) [years]
• T_{Life_Profile} is the estimated battery lifetime for the customer's temperature profile [years]

For the case of the temperature holding a finite number of discrete values, Equation 2 can be used to compute the conversion factor.

Eq. 2

where

• K is the nominal lifetime conversion factor [unitless]
• T_i is the temperature during the i^th time interval [°C]
• t%_i is the percentage of the battery lifetime at a temperature of T_i [hours]
• A(T_i) is aging function that corresponds to the battery in question [unitless]

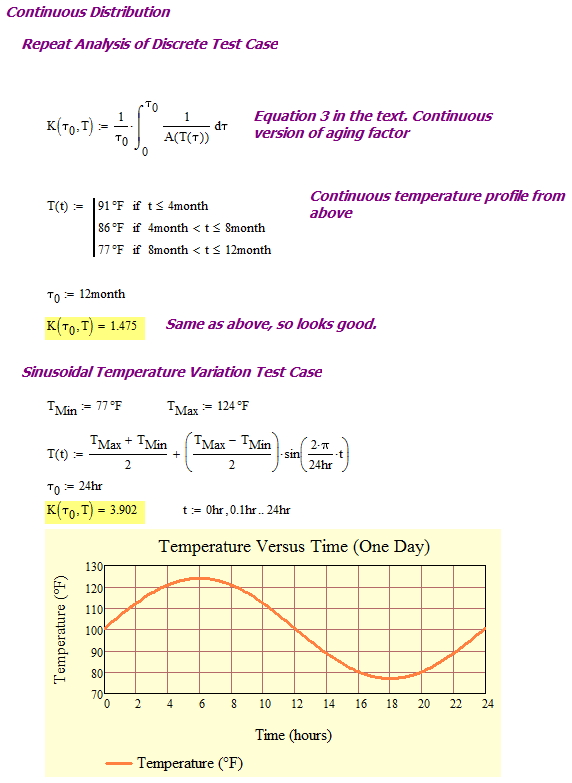
For the case of a continuously varying temperature environment, Equation 3 must be used.

Eq. 3

where

• t_i is time [hours]
• τ ₀ is the interval of integration over the profile time [hours]
• T is the duration for the application of the temperature profile [hours]
• K is the duration of the time interval with a temperature of T_i [hours]

You can view as representing the percentage of time represented by a differential length of profile time. As in the discrete case, you can view this as the computing of a weighted average.

Analysis

Discrete Temperature Distribution

Figure 1 shows my evaluation evaluation of Equation 2 for the discrete temperature profile used in the paper by McCluer. I obtained his result, so I have verified my Mathcad implementation.

Figure 1: Analysis of a Discrete Temperature Distribution.

Continuous Temperature Distribution

Figure 2 shows my evaluation of Equation 3 for a both the discrete temperature profile used in McCleur's paper and for a continuous temperature variation based on a sine wave (I could have used anything). I am assuming that every day has the same temperature variation. Thus, the percentage of time spent at each temperature is the same for each day and for all the days in total. If I wish to use a period of time longer than a day, I simply extend my interval of integration over the period of time desired.

Figure 2: Aging Analysis for a Continuous Temperature Variation.

Conclusion

I recently went through this exercise while assisting a customer in a desert climate. They were trying to estimate the effect of temperature on their battery replacement costs. My analysis gave them a rationale approach for determining their operational costs.