Introduction
I frequently get very specific questions on my posts. Normally, I simply reply directly to the question. One recent question required an answer that I thought might be interesting to a broader audience.
Background
Here is the question that I received on this post. This post contains my review of work by Pejsa that presents simple algebraic expressions for projectiles experiencing aerodynamic drag.
Has anyone provided a physical explanation for Pejsa’s “retardation coefficient”? I suspect I know what it actually represents, but I’m not sure.
I frequently need to include parameters in my system models, and I frequently end up staring at these parameters and asking "what do they represent physically?" This post will show the thought process that I go through to provide some physical meaning to these numbers.
Analysis
Pejsa derived the following expression for how a projectile's velocity varies with range (Equation 1).
| Eq. 1 |
where
- r is the projectile's range.
- V is the projectile's velocity at range r
- F0 is the retardation coefficient at the time of projectile launch.
- n is a modeling parameter that is function of the velocity of the projectile.
- V0 is the projectile's initial velocity.
The reader's question is focused on interpreting the meaning of F0. Figure 1 shows my derivation of a simple expression that shows me that F0 is analogous to the time constant of an RC circuit. F0 represents that distance at which the projectile's velocity has dropped to 1/e of its initial value.
Pejsa used a slightly different approach to interpreting F0, which I show in Figure 2.
Here is a quote from Pejsa's "Modern Practical Ballistics" that describes his interpretation.
As an example, for a bullet to have a retardation coefficient F equal to 2700 [feet] means that for 27 feet (1 percent of 2700), the bullet loses 1 percent (or retains 99 percent) of its remaining speed to air drag. It can be said that that the speed of the bullet "decays exponentially" at a rate of 1 percent for every 27 feet.
This statement is completely consistent with what I derived in Figure 1. In fact, a completely analogous statement can be made for RC circuits.
Conclusion
This is just a quick post to help a reader develop some physical insight into the meaning of a number. Engineers are always looking for insight into numbers. I am reminded of my favorite quote on computing and insight by Richard Hamming.
The purpose of computing is insight not numbers.
For me, I do not really understand a concept until I can describe how it behaves without having to resort to mathematics. A physical interpretation of the modeling parameters helps with developing intuition.



Pingback: Modeling Drag — Projectile Velocity Versus Range | Math Encounters Blog
Do you know of a table or list that contains either the standard form factor or the BC of the G1 thru G7 standard projectiles? I can find the G1, but none of the others.
Thanks in advance
Tony
Thank you for this. I understand that the dimensions are:
k is 1 / distance
F is distance
What are the units of n please?
Sorry it's non dimensional
But when I use the formula
F = 1 / (k * v0^n)
n = 0.266
I get the wrong units for F; ((distance^149/203)(time^54/203))
I am a bit tied up today for a detailed answer, but take a look at this example.
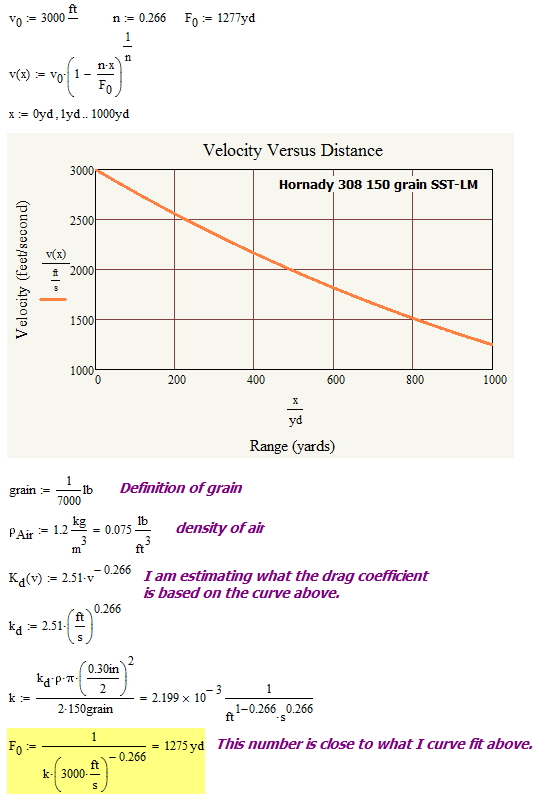
n is unitless.