Introduction
I received an email this weekend from a dad struggling to help his son with a project involving aerodynamic drag and BB gun. I did some quick calculations which I document here. I will try to look at pellets tomorrow. I was able to use basic principles to duplicate the empirical results quoted by manufacturers.
I will be computing three numbers associated with an air rifle shooting a BB:
- The force of drag on the BB as it leaves the muzzle
- The deceleration of the BB as it leaves the muzzle
- The ballistic coefficient of the BB
Background
Definition of Ballistic Coefficient
The Wikipedia defines the ballistic coefficient as follows:
- Ballistic Coefficient
- The Ballistic Coefficient (BC) of a body is a measure of its ability to overcome air resistance in flight. It is inversely proportional to the negative acceleration — a high number indicates a low negative acceleration.
A projectile with a small deceleration due to atmospheric drag has a large BC. Projectiles with a large BC are less affected by drag and have performance closer to their performance in a vacuum.
While the Wikipedia definition is accurate as far as it goes, it does not allow you to compute the BC of a projectile. Equation 1 shows you how to compute the BC of any projectile.
| Eq. 1 |  |
where
- aReferenceProjectile is the acceleration of a reference projectile (eg. G7).
- aProjectile is the acceleration of the projectile we are interested in.
Coefficient of Drag Given Reynolds Number
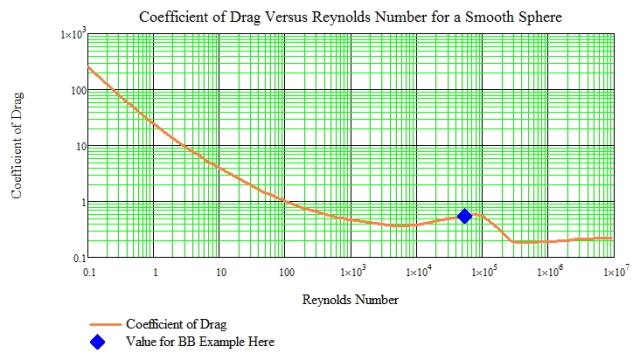
Figure 1 shows the coefficient of drag graph that I digitized using Dagra for this example.
Figure 1: Coefficient of Drag Versus Reynolds Number.
Density and Viscosity Data for Interpolation
Figure 2 shows the table from this web site that I interpolated so that I could get the density and viscosity of air at various temperatures.
Figure 2: Air Density and Viscosity Data.
Analysis
Interpolation of the Air Data
Figure 3 shows how I used Mathcad to interpolate all this data.
Figure 3: Digitization Code for Graphical Data.
Calculations
Figure 4 shows how I calculated the
- force of drag on the BB
- acceleration experienced by the BB
- ballistic coefficient of the BB
Figure 4: Calculations for the Drag and Ballistic Coefficient of a BB.
Conclusion
I computed three numbers associated with an air rifle shooting a BB:
- The force of drag on the BB as it leaves the muzzle: 0.17 N = 0.038 pound = 0.613 ounce
I cannot find corroborating information on the web. However, I use this number to compute the ballistic coefficient, for which I do find corroborating evidence.
- The deceleration of the BB as it leaves the muzzle: 1691 ft/sec2
Straightforward application of Newton's second law.
- The ballistic coefficient of the BB: 0.014
Next, I will look at a 22 caliber pellet.
Pingback: What Is The Best Ammo For Air Rifles? |IDF (Zahal)
Pingback: Different Types of Airgun Pellets - Outdoor Empire
Very good, but the ballistic coefficient (BC) of a projectile is a function of its velocity; therefore, the published BC is an average used for the intended range for the distance the manufacturer or publisher thinks the projectile will arrive on target. Now, a Crosman copper coated BB is closer to 5.00 grains than 5.10 grains and the diameter is much, much closer to 0.17175+/-0.00025 inch than the erroneously named caliber of 177. To begin, caliber is a measurement of hundreds of an inch and not thousandths. It's as erroneous as saying water freezes at 273.15 degrees kelvin (there are no degrees in kelvin temperatures). Your values are very close to accuracy, but you cannot have precision unless you weigh and measure every BB. Also, Daisy and Crosman BBs are among the best and economical BBs to be obtained, but they can vary two to sometimes three thousands of an inch in diameter. The alleged "flyers" are mainly too heavy or too light outlier BBs. For precision and testing purposes, it is best to buy a quality 11/64-inch drill bit and drill a hole in steel plate at room temperature to make a Go-No-Go BB gauge and at least seperate the lot into lighter and smaller diameter with the BBs that fall through the hole, and you will be amazed at the precision and accuracy improvements. Thank you for your analysis.
Drag calculation is off a tad. Based upon a Reynolds number of 53,000 and Figure 1, the coefficient of drag is slightly less than 0.2 - not the 0.549 value you report. Because it is a log graph, Re= 53,000 is located about two-thirds the way to 1 x 10^6 from 1 x 10^5. Hence, your X is marking the wrong spot - in the coefficient of drag graph.
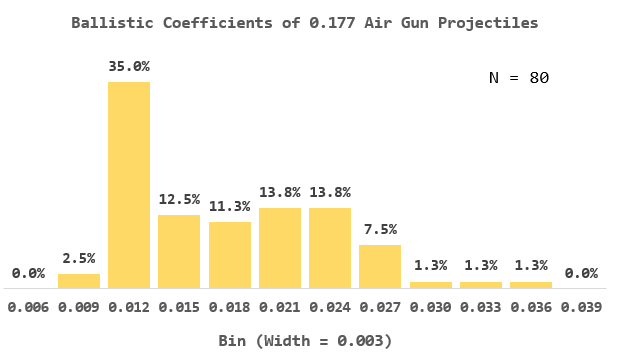
Thanks for the comment. 53K is about 2/3 the way between 10K and 100K on a log scale, which the graph shows. So I am a bit confused. I believe that my BC calculation is correct. I did take a look at a fair number of 0.177 and 0.22 projectiles to make sure my values were the correct order of magnitude. For example, here is a histogram for the measured BCs of 80 0.177 projectiles. My BC calculation of 0.0145 is reasonable.
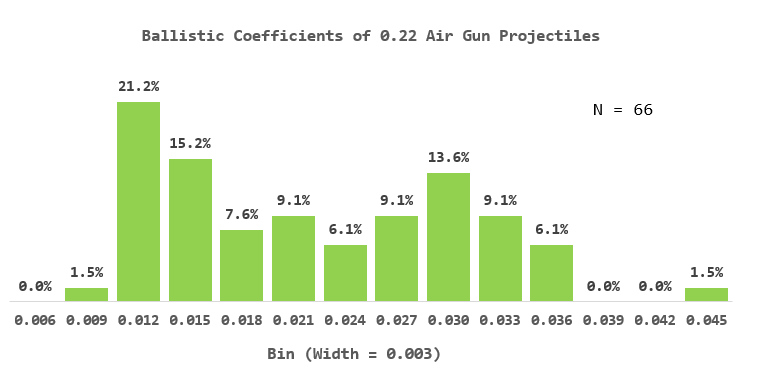
Here is a similar plot for 0.22 projectiles.