Quote of the Day
The only hope of a pure mathematician is to die before their work is applied.
- Pure mathematician stunned to hear that his work found an application in string theory.
I am considering building a small structure at my lake cabin that has a hip roof. Now a hip roof is pretty awesome, I'm considering consulting with someone like Mars Restoration to find out all the ins and outs and how I can build this structure in compliance with a roof like this. It's been on my mind for a while. When I bought the cabin, it was pretty run down and in need of a lot of repairs but because of other commitments, I had to hire a contractor and a roofer in Wilmington, DE to do most of the work for me. They did a good job but as you know, I'm a big fan of DIY so I'm wanting to build this structure myself.
Obviously, I don't have as much experience as the roofer I hired for my cabin so I've had to do a lot of research into this, looking into companies similar to 99Roofers to see what they offer. If I did do the roof myself there was a good chance that I would miss something important and later witness the roof coming down. The structure will look a little bit like the one shown in Figure 1 but with a steeper roof pitch. This roof has a 3/12 pitch whereas I'm looking for more of an 6/12 roof pitch.
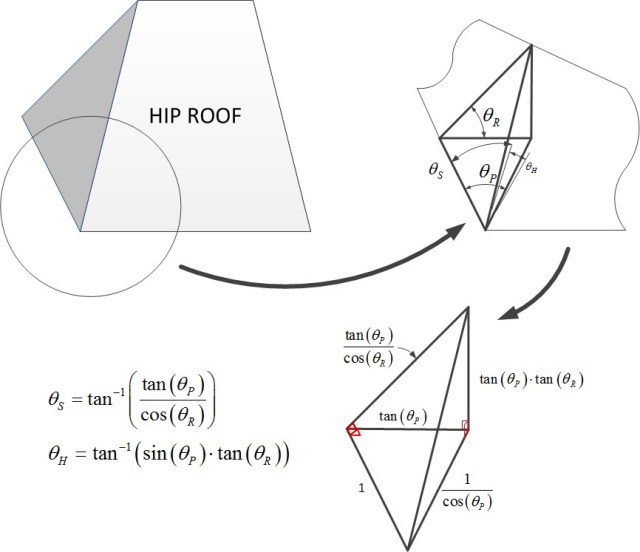
To build this structure, I need to compute a few angles and, unfortunately, I have forgotten how to determine them using a steel square. To derive formulas for the critical angles, we need to define some terms, which I do in Figure 2. Using these angle definitions, I will derive formulas for the sheathing (?S) and hip pitch angle (?H) given the common pitch angle (which I call the roof pitch [?R]) and plan angle (?P).
Figure 3 shows my derivation. The derivation uses basic geometry, so I will just let the drawing stand for itself. If more detail is needed, send me a note. I will use this post to document formulas as I need them.
I did find formulas for these angles presented on this web page, but no derivation was given ? that's no fun at all!



little help for calculations http://myrooff.com/hip-roof-calculator/
It seems it's difficult to calculate the Hip roof area
Helping for Roof Pitch Calculator
http://roofgenius.com/roof-pitch-calculator.asp
Helping for Hip Roof Angle Calculator
https://roofgenius.com/roof-pitch-calculator.asp
Surely it must be possible to apply a simple multiplier to the pitch angle, say 30 deg., to derive the hip angle ??? like .75, so 30 x .75 = 22.5deg. Does anyone know what the 'normal' multiplier might be, where the hip pitch is the same as the main pitch?
We know all you maths nerds are geniuses, thanks a lot, but just give us the number, not the symbols!!
What carpenter will use trig to work it out!!!
Site work is practical, not a maths workout!!
hi there iam trying to make a 4 sided roof for a lantern , but i can not find how to cut the sides of each piece , the staces are 8 inches at the bottom and up to a point at the top , the 4 staces just will not fit together , iam retired and not good with math , if you have any angle that i need to cut the staces , thank you for your time