Drawing a Perpedicular Out in the Wild

Figure 1: My Paver Patio and My Need for an Accurate Perpendicular.

My most satisfying applications of geometry occur in my construction projects. Previously, I have discussed how to find the radius of circle on construction projects. In this post, I will discuss four methods for constructing a perpendicular to a line. The forth method is one is new to me and dates back to the Mayans.

I recently had to replace a concrete patio that had become terribly cracked. I solicited bids from contractors, but their bids were five times the cost of building the replacement patio myself – this was too much for me to pay. I was that set on the fact that I wouldn't be paying this much money that I started to look for alternative options. I'd been told that decking would work wonders in a yard like mine, and so started to look for companies similar to this uk decking supplier to see what types of materials they had so I could get everything in place. However, I quickly came to the realization that a new patio was something that I had set my mind on ever since my old one fell apart so I felt like I had to go through with this particular renovation after all. Even though it was a bit more than what I wanted to spend. Yes, I am cheap and I frequently suffer from sticker shock. My thrift is a legacy of my German father and grandfather. So I decided to lay my own paver patio – of course, I have never laid a paver before. I had to check with my home insurance to make sure that I was covered in case any damage happened to my property, it's always best to find good companies that give you the best insurance deal for you, always look around! Anyway, back to the patio.

Figure 1 shows a corner of my new paver patio. As you can see in the photo, the patio is placed between my house and my driveway. It includes a structural post that holds up part of my roof.

The patio was a bit tricky to layout because:

• The concrete patio abutted my concrete entry steps, my house, and my driveway.

  My paver patio is going to be rectangular. So I need to layout out perpendicular lines from my house.

• I wanted only full rows of bricks.

  I did not want to cut large number of pavers to size. I think full rows look better than partial rows and cutting pavers is slow work. This means that my paver patio will be slightly larger than my old concrete patio and I will need to cut a straight line into my asphalt driver. It turns out that cutting a straight line in the asphalt was slow, but not difficult – I just needed a special blade for my circular saw. If you want more details on how to cut asphalt, see this fellow's blog post.

• I want water to run away from the house.

  This means that I need the pavers to slope down from the house to the driveway.

• The original structural post had rotted.

  The base of the column had been buried in the dirt and it rotted – not the way to install a column. This meant I need to establish a footing and put in a new column. While this is not pertinent to finding a perpendicular, it did complicate the installation of the patio.

Figure 2: Bosch Jack-Hammer that I Rented.

I needed to construct a perpendicular line from the end of my house to a point on the driver that was an integral number of paver rows from the house. Unfortunately, the edge of my house is not well-defined because it consists of bricks that are not all flush sitting on a concrete pad that was attached to the old concrete patio. So I had to rent a jack-hammer (Figure 2) and spent an entire day removing the old patio. This effort was made more difficult because the concrete was reinforced with a steel mesh. When I jack-hammered (Figure 2) the concrete patio out, a jagged concrete edge was left along the edge of my house and steps. I set the top level of the pavers to cover the rough edge.

I began my layout by establishing a line along which my first row of pavers would line up. I simply made a line that was as straight as I could along the jagged concrete edge along the house and my steps.

With the lines along my house and steps serving as my baseline, I only had two more lines to draw: (1) A line parallel to my house on my driveway along what would become the long-side edge of my paver patio rectangle, and (2) a line perpendicular from the edge of my home to the line drawn on my driveway, which represents the short-side edge of my patio rectangle.

My approach to constructing these lines was simple:

• Draw two lines that extend onto my driveway that are perpendicular to my house baseline.
• Mark points that are an equal distance on each perpendicular at the outside paver edge.
• Connect the two points for the outside paver edge with a line.

I know of four methods for constructing a perpendicular line. I ended up using method 1, but I thought it was worth writing the other three down.

Method 1: 3-4-5 Triangle Method

The classic method of determining the perpendicular to another line is usually called the "3-4-5 Triangle" method but it works for any Pythagorean triple. Figure 3 illustrates this method using a 6-8-10 triangle.

Figure 3: Illustration of the 3-4-5 Triangle Method.

This is the approach that I actually used.

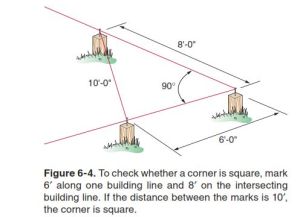
Method 2: Shortest Distance from a Point to the Line

Let's start the discussion with a definition:

The distance from a point to a line is the shortest distance between them, which is the length of a perpendicular line segment from the line to the point.

Figure 4 illustrates the approach. You use a tape measure to find the minimum distance to the line. This approach would not work well in my situation because my house wall would interfere with measuring the minimum distance accurately.

Figure 4: Minimum Distance Method.

I have used this method when I am in a hurry.

Method 3: Bisector of an Isosceles Triangle

Working similar to method 1, we can draw a isosceles triangle and bisect the base. A line drawn from the vertex to the bisection of the triangle's base is perpendicular to the base. The technique is based on the following theorem (proof).

A point is on the perpendicular bisector of a line segment if and only if it lies the same distance from the two endpoints.

Figure 5 illustrates the process (source).

Figure 5: Bisecting an Isosceles Triangle.

Method 4: Mayan Rope Technique

I saw this method described on the +Plus magazine web page. I thought it was pretty clever. Here is a video that shows some students applying the Mayan technique.

If you're interested in learning more about concrete patio building, a friend recommended https://sealwithease.com/10-tips-for-building-a-concrete-patio/. This article provides some useful tips for making the right patio.