Quote of the Day
Russia is a riddle wrapped in a mystery inside an enigma.
— Winston Churchill.
Introduction
While reading a web page on WW2 naval warfare, I found some interesting material on how naval gunfire was spotted -- the process for correcting aiming errors. This web page contained Table 1, which indicates the maximum range at which an observer 100 feet above the waterline on a ship (called "own ship") can see another ship (called "target") of a given height above the waterline.
|
Range (yards) |
|
|
10 |
30700 |
|
20 |
33600 |
|
30 |
36100 |
|
40 |
37900 |
|
50 |
39700 |
|
60 |
41300 |
|
70 |
42800 |
|
80 |
44200 |
|
90 |
45400 |
|
100 |
46600 |
|
110 |
47600 |
|
120 |
48900 |
I can regenerate Table 1 using the distance-to-the-horizon equation I derived in this post. I thought this would be a nice application example.
Let's dig in ...
Background
Table 1 assumes that we are limited to seeing objects that are visible optically on the horizon assuming refraction. Before radar, battleships had all sorts of optical measuring instruments for detecting targets and measuring their range. Figure 1 shows a battleship photograph that calls them out (Source).
Figure 1: Optics Deployed on the USS Idaho.
For battleships to engage targets at long range, they needed to be able to accurately determine the range to targets and optical rangefinders were an excellent solution prior to the arrival of radar. In this post, I want to take a closer look at how rangefinders worked. The original concept for these naval optical rangefinders was developed by Bradley Fiske, a naval technologist that few people know about today. I read his biography and was very impressed with the scope of his inventiveness.
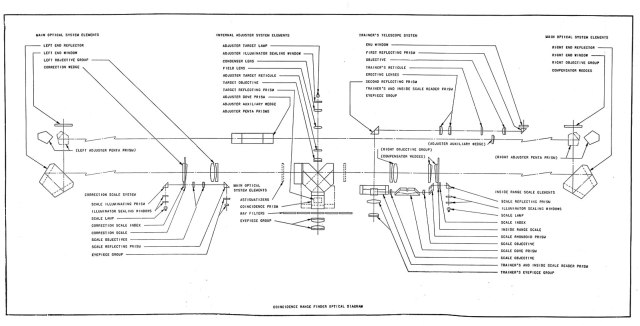
There were many variations on the basic rangefinder idea. For my purposes here, we will look more closely at the variant known as a coincidence rangefinder. Figure 2 shows a block diagram of a coincidence rangefinder (Source).
Figure 2: Block Diagram of a Coincidence Rangefinder.
There are two prisms (actually called pentaprisms) at the end of two long arms -- each arm often 4 or 5 meters in length. The design brings the images into coincidence by rotating the compensating wedge prisms. In theory, they could have rotated one of the pentaprisms to bring the images into coincidence, but it turns out that is difficult to do accurately on targets at long range. The compensating wedge prisms provide a more accurate solution. There are numerous subtleties in the construction of these devices that are beyond the scope of this note. See the source for some of the interesting details. The compensator prism wedges and their function are particularly interesting.
These rangefinders were quite large and were often armored. Figure 3 shows a rangefinder from the Graf Spee, a German "pocket" battleship (Source).
Figure 3: Rangefinder from the Graf Spee.
The following quote nicely describes its function (Source).
The coincidence range finder uses a single eyepiece and uses a prism to merge images from both lenses into a single image to present to the operator. The operator adjusts the rotation of the prisms using a dial until the images overlap in the eyepiece. The degree of rotation of the prisms determines the range to the target by simple trigonometry.
The operation of the pentaprisms is interesting. Figure 4 contains a nice illustration of how the light bounces around a pentaprism (Source).
Figure 4: Light Bouncing in a Pentaprism.
The basic geometry involved with a coincidence rangefinder is simple enough. Figure 5 shows that the coincidence rangefinder determines range using simple Euclidean trigonometry (Source).
Figure 5: Coincidence Rangefinder Geometry.
Here is another drawing that does a nice job of illustrating how the rangefinders were constructed (Source).
Figure 6: Top View of an Optical Rangefinder.
For those of you interested in how the rotating prism can support precise angular measurements, see this comment for details.
Analysis
Strategy
Here is my analysis approach:
- Develop a formula for the maximum range of an optical rangefinder
I will assume that the observation height above the waterline is what limits the maximum range of the rangefinder.
- Determine the refraction radius that the US Navy used.
The maximum range will be affected by refraction. This post gives us a way to model the refraction by using a refraction radius.
- Compare my results with the results listed by the US Navy.
I will examine the differences between the US Navy's table and the equivalent table generated by my formula.
Optical Rangefinder Maximum Range Formula
Equation 1 shows the formula for determining the range to the horizon assuming refraction (from this post).
| Eq. 1 |  |
where
- rE is the radius of the Earth.
- rR is the radius of the refraction circle.
- h is the height of the observation point.
- s is the arc length from the observation point to the horizon.
Figure 7 shows the maximum range scenario that a battleship would experience with a target. We will apply Equation 1 twice to determine the maximum rangefinder range.
Figure 7: Optical Geometry for Analysis.
Using Figure 6 and assuming each ship just sees the other on the horizon, we can determine the maximum range using Equation 2 -- which uses Equation 1 twice.
| Eq. 2 |  |
 |
where
- H is the height of the rangefinder.
- h is the height of the target.
- sO is the arc length from my own ship to the horizon.
- sT is the arc length from the target ship to the horizon.
US Navy Refraction Radius
This is an error minimization problem. I can write a routine that finds the refraction radius that minimizes the error between my formula (Eq. 2) and the US Navy's table. Figure 8 shows my Mathcad routine form performing this minimization. I minimized the maximum error. You could also minimize the maximum percentage error -- the answers are very similar.
Figure 8: Determination of Refraction Radius Used By US Navy.
Error Between My Formula and the US Navy Table
Figure 9 shows my comparison between the US Navy result (Table 1) and my formula (Eq. 2). The agreement is very good considering they probably used slide rules for their work. I shudder thinking of my own youth when I had to use slide rules.
Figure 9: Comparison by US Navy Rangefinder Table and My Formula.
Conclusion
I showed that the US Navy table and my formula produce results that are within 0.3% of each other for a refraction radius that is 6.975 that of the Earth's radius (they probably just used 7). This accuracy is reasonable assuming they were using a slide rule for their computations.
In Figure 10, I thought I would add an excellent picture of a rangefinder from a US Navy ship's fire control system to show how their appearance could vary (Source).
Figure 10: Rangefinder incorporated in Mk19 Fire Control System on USS Pennsylvania (BB 38).
If you are looking for more information on WW2 rangefinders, here is a manual. It is a large file (>7MB).
Pingback: Battleship Rangefinders and Geometry | Blog
I guess that once you take into account waves that error term doesn't make too much impact. It would be interesting to know how much height a ship gains/loses in waves, and how big a wave would have to be to impact these calculations (I guess this depends upon the mass and potentially centre of mass)
As used in this post, target height is the difference between the highest point on the target and the water line. The target height was only important for determining visibility of the ship. It was not important for determining range.
Depending on the type of device being used, the observer would see two images of the ship in his viewer. He would then either (a) superimpose the images on top of one another or (b) line them up vertically. The fact that the ship was going up and down on the ocean would not matter. With the images aligned, the two pentaprisms were pointing at the same object and the target range could be read from a scale. Target height did not enter into the range calculation.
Mathscinotes
Pingback: links of the week – 22 July 2014 | a blog
I am interested in the mechanical aspect of the adjustable prism assembly. I must assume that the angle to target would be very small even with a distance of 30-40 feet from prism to prism. If that is the case the measurement of the angle needed to be very precise to accurately determine the length of the adjacent triangle leg. What information do you have about the gears, scales and associated mechanical devices used to measure the angle?
Hi Gregory,
I had hoped to blog about the details of how the wedge prisms are used, but I simply have not had enough time. However, I think I can give you some pretty good references that will show you how they work. It is pretty cool!
I still want to go through the math involved, but I do not know when I will have time.
mathscinotes
Have you any information on the possible error caused by thermal lengthening-shortening of the measuring arm, since in dealing with such small angles any change in length of the measuring arm must introduce at least some error. Were there tables or other references for dealing with this possibility?
I haven't seen any data on temperature corrections. The design of the units did incorporate elements to minimize temperature-induced errors – link with a sentence mentioning temperature isolation. So it sounds like temperature-induced errors were a concern and designs were developed to minimize those errors.
mark
Thank you.
How was the coriolis effect calculated or wasn't it considered significant?
The Coriolis force is not involved with distance measurement, but does affect projectile motion. The Coriolis force is a fictitious force that appears to occur when a projectile's trajectory moves across a a rotating frame of reference, like the Earth.
For those who are not familiar with the effect of the Coriolis force, the Wikipedia has an excellent description. Its is only significant on very long range artillery pieces, with the Paris Gun being the most famous case. Battleship gun directors usually compensated for the effect, but it normally is small.
mark
Pingback: Earth’s Curvature and Battleship Gunnery | Math Encounters Blog
Also what about distance, inevitable variance of ammo weight, Powder and explosive speed error? IF a round that weight 50 lbs at 3000 Fps, compared to a 51 lbs round flying at 2926 Fps because it was machined differently? Is it incorporated into today's Radar guidance, sensors and algorithmic Math? It used to take 7 rounds to hit a ship at a distance, now it is like 1 or 3 max.
Achieving a repeatable one-shot hit capability requires compensating for many things. For example, the age of the smokeless powder has an effect. During WW2, battleship shot-to-shot velocity variation was ±10 feet per second (fps). The same powder used by the USS New Jersey during the 1980s produced ±32 fps shot-to-shot velocity variation (Source). This velocity variation results in a 2100 yard average pattern size at 35,000 yards (Source). In fact, this velocity variation has been blamed for the New Jersey's poor gunnery during the Lebanon action. Some systems try to correct for this variation. The WW2 cruiser Prinz Eugen had a system to measure shell velocity and to add a correction – very advanced for the time. Because the steel barrel droops as it heats up when fired, the M1 Abrams fire control system measures barrel droop and corrects for the error. All this information and more (i.e. Coriolus effect, Earth's curvature, barrel wear, meteorological conditions, etc) must be accounted for in a firing solution. Modern computers make these corrections relatively straightforward to make.
As you mention, each shell has an intrinsic variation that the fire control system cannot remove. For example, the Rheinmetall DM53 APFSDS (used by Germany with its 120 mm tank gun) has an intrinsic dispersion of 0.2 milliradians (i.e., 20 cm at 1000 yards). The 16-in/50 cal Mk 7 guns on the Iowa class had a shell-to-shell dispersion of 0.36% of total range, which is 3.6 milliradians.
mark
Hi, this rangefinder fascinated me too. I am looking to construct a similar rangefinder that works on rivers. This is for a dolphin survey where the observer needs to determine how far the dolphin surfaced from him/her. Laser ones don't work on it. something like the coincidence rangefinder would be useful, I thought. Any inputs from you will be useful Thank you.
Hello Aaranya,
I collect Rangefinders from Musketry Rules c.1850s through to cold-war Stereo Optical rangefinders up to the late 1980s; and would initially suggest that you look on a few online auction sites for a handheld rangefinder made in the 1970s/1980s made by 'Ranging Inc.' They have a range instruments for hunting and various other leisure and semi-professional use that can measure up to 1000 meters/yards; but beware that some of the smaller model numbers relate to distance max. in feet, and not meters/yards. If you can, look for the 1000 model (in yards/meters) in white, or grey plastic. All of these single-eyepiece instruments work on the same co-incidence principle, but some are also equipped with a clip-on eyepiece magnifier, so look for a model with that option if possible.
I'm assuming that you need something light and portable as a trial initially (assuming that distance measurement within 1000 metres is acceptable), but if you are shore-based and need longer distances then you're entering the realms of ex.military WW1 / WW2 instruments, or post-war instruments where size/weight and cost will vary considerably. Best to avoid Stereoscopic rangefinders as they can be difficult to get used-to.
Best of luck with your quest, your application sounds quite fascinating. Please let us know how you get-on.
Regards,
Paul
It's not a matter of slide rule. It's just a matter of simplify. Observe that the 2 right decimal cases of the Navy table are just ZEROs.
Hi Mark,
I was looking for a guide on how to work a battleship aiming system when I stumbled upon your blog. I found it to be a precious small trove.
I have interests in everything World War II, and I play a lot of such games.
Do you, by any chance, be familiar with what I'm looking for - working with a battleship aiming system? My math is terrible, and I couldn't figure out even the simplified calculation of it.
Hi Andy,
I have done quite a bit of work on submarine and artillery fire control, both professionally and in a gaming context. I am currently working right now on an app to teach people how to aim straight-running torpedoes (WW2 era) using the technology of the time. If you can form a question, I might be able to help. I realize it is hard to even know what to ask when you first start – that is how it was for me.
mark