Kepler Planet Finding Probabilities

Quote of the Day

To finish a task, you first must start it.

— Gary Ronneberg

Introduction

Figure 1: Planetary Systems with Different Orientations.

One of my favorite online magazines is +Plus. I was reading an article in +Plus today about how the Kepler satellite finds exoplanets and the article mentioned a simple formula for the probability of Kepler being able to detect a planet. I thought it would be interesting to discuss this formula here because it involves a simple formula that provides insight into cutting-edge science.

The article was written by Marianne Freiberger, whose written work for +Plus is excellent. Actually, all their math writing is excellent. Check them out.

Background

Planetary Systems with Different Orientations

Figure 2 shows an image from NASA/JPL that shows two adjacent planetary systems in different orientations.

Figure 2: Image of Actual Solar Systems with Different Orientations.

Kepler Planet-Hunting Concept

The basic idea behind the Kepler planet hunting concept is a satellite can detect the dip in optical power level seen from a star when a planet passes in front of it. A planet passing through our field of view is called a transit. Figure 3 illustrates this concept (source).

Figure 2: Planet Transit and Light Level.

Figure 3: Planet Transit and Light Level.

This approach does have shortcomings:

The light level dip is very small.
Detecting a planet with the size and orbital of Earth about a large star requires a very sensitive instrument. I will compute the level of optical power reduction that the Earth transiting the Sun would provide to an alien observer.
The solar system we are looking at must be oriented toward our solar system so that its planets cross the face of the star.
Many solar systems are not oriented relative to us in a way that their planets will ever transit the face of their star.
Because many planets orbit their stars slowly, many planets will require years of observation to find.
Few planets have been imaged directly. Most are found by indirect methods that take years of observation to detect planets.

Analysis

Article's Equation

The +Plus article stated Equation 1 for the probability for the transit of a random orbit to be visible about a star.

Eq. 1

$\displaystyle {{P}_{Transit}}=\frac{{{D}_{Star}}}{{{D}_{Orbit}}}$

where

P_Transit is the probability of planetary transit by random orbit.
D_Star is the star's diameter.
D_Orbit is diameter of the planet's orbit.

I had not seen this equation before and I thought it would be useful to derive it here.

Approach

My approach will be simple:

Develop a model for the different types of orbital orientations.
Determine the set of orbits that will transit the star when seen from Earth
Determine the probability of an orbit passing in front of a star when viewed from Earth

Orbit Orientation

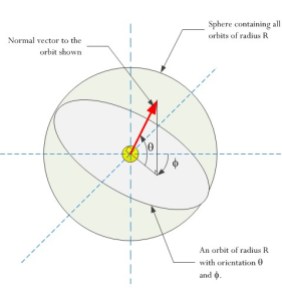
Figure 3: Orbital Orientation Specification.

Figure 4: Orbital Orientation Specification.

Figure 4 illustrates how you can specify any orbit of radius R with two angles, θ and φ. These angles simply provide the orientation of a normal vector to the orbital reference plane.
I will first compute the probability of an orbit transiting a star by holding one of the angles, say θ, constant and letting φ vary across its range. It does not matter which θ I hold constant because we have spherical symmetry here. Since we have spherical symmetry and I arbitrarily chose the angle θ to hold constant, all the θs will have the same probability of transit. Since they all have the same probability of transit, the overall probability of transit is the same as for one orbit.

Transit Probability

Derivation

Figure 4 shows how we can compute the probability of a transit for a given set of orbits. I will break problem up into three parts:

Consider the set of all orbits of radius R that have a single angle parameter (θ) held constant.

Figure 5(A) shows this case. There are an infinite number of orbits with this orientation and we can see that probability that an orbit transits the star is related to the:

Diameter of the star
Diameter of the orbit

Compute the percentage of these orbits that will transit the star.
Each orbit in the set can be described by its y-axis intercept. All orbits with a y-axis intercept less than the radius of the star (R_Star) will transit the star. This means that the percentage of orbits that will transit the star is simply $P_{Transit}= \frac{R_{Star}}{R_{Orbit}}=\frac{D_{Star}}{D_{Orbit}}$ , which I illustrate in Figure 5(B).
Observe each orbit set with a different θ will have the same probability of transit.
Figure 5(C) illustrates a few different θ values. Since all θ values have the same probability of transit, this means the overall probability of transit is given by $P_{Transit}= \frac{D_{Star}}{D_{Orbit}}$ .

Figure 4: Illustration of Different Orbital Orientations.

Figure 5: Illustration of Different Orbital Orientations.

Example

Figure 5: Probability of Detecting Earth.

Figure 6: Probability of Detecting Earth.

Figure 6 shows how we can compute probability that an alien observer would be able to use the transit method to detect Earth about the Sun. The percentage is ~0.5 %, which is pretty small. This means that to detect many planets, you will need to look at many stars. In fact, Kepler looks at thousands of stars. Here is a quote from the NASA's Kepler page.

Data from the US Naval Observatory digitization of the Palomar Observatory Sky Survey (USNO-A1.0) (Dave Monet, 1996), complete to M_V[Visual Magnitude]=18, was used to determine that the actual number of stars with M_V<14 of all spectral types and luminosity classes in the 105 deg² FOV[Field of View] to be 223,000. About 61%, i.e., 136,000, are estimated to be main-sequence stars. Prior to launch high-resolution spectroscopy was performed to identify and eliminate the giant stars in the FOV. During the first year of the mission, the 25% most active of the dwarf stars were eliminated reducing the number to 100,000 useful target stars.

I do find it interesting that they filter out active dwarf stars. I guess that makes sense -- if the star's brightness is varying, how do you know if it was because of a planet transiting or just something that star does (see NASA page on this topic).

Amplitude of the Dip

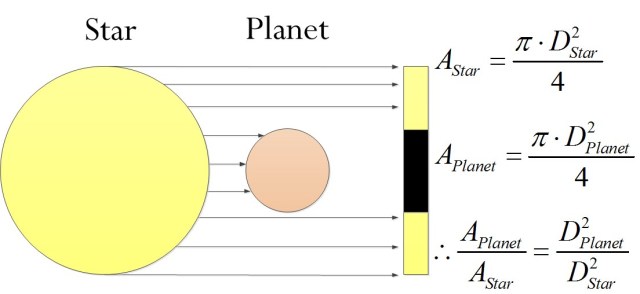
The optical power we see from a star will dip slightly when a planet passes between the star and the Earth. As an example, we can estimate the optical power dip for the Earth in front of our Sun by realizing that when the Earth passes between the sun and the observer, the total visible optical power will dip by the ratio of the circular area of the Earth to the circular area of the Sun. Figure 7 illustrates how this dip can be computed.

Figure 3: Illustration of Dip Calculation.

Figure 7: Illustration of Dip Calculation.

The calculations in Figure 8 show show that dip for the Earth transiting the Sun is about 1 part in 10000 (as stated in Marianne's article).

Figure 4: Computation of Sun Dimming From Earth's Transit.

Figure 8: Computation of Sun Dimming From Earth's Transit.

Conclusion

I have been reading about the Kepler planet-finder for years, but I have never worked through any numbers on what it is doing. This was a good exercise that provided me some insight as to the difficulty of the problem they are dealing with.

M	T	W	T	F	S	S
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30
31