Optimum Television Viewing Distance

Quote of the Day

I am not a fast reader, I am a fast understander.
— Isaac Asimov

Introduction

Figure 1: TV Viewing Distance Versus Resolution.

My wife has said that we are going to move into the 1990s and buy a High-Definition TV (HDTV). I am not an early adopter of any technology. Yes, I have been called a Luddite.

Among the many features to choose is the screen size. The television will go into a room that has a maximum viewing distance of 10 feet. How do we go about choosing the the screen size? I told my wife that that there are many approaches to determining the proper viewing distance. I thought I would document this discussion here. While her eyes glazed over about half-way through the discussion, you might find it more interesting – you are reading a math blog after all.

Figure 1 shows a commonly seen chart of the size of the screen versus versus viewing distance. I will show how to generate this chart for yourself. I will derive an expression for the minimum viewing distance assuming that you want the television's pixel detail to be indiscernible to the human eye.

Background

Television Basics

I covered most of the basics of television in this post and I will refer you there if you want to know more about pixels and resolution.

Viewing Distance Theories

The Wikipedia has an excellent discussion of this topic and I will refer you to that article for all the nuances associated with this topic.

The most common approaches that I see people use for determining the proper viewing distance are based on:

• human visual acuity

  Most of these recommendations assume that the human eye cannot resolve any details finer than 1 arc–minute, a rough but defensible standard. Figure 1 is based on this approach.

• viewing angle

  Commonly used angles are 20°, 30°, and 40°.

• THX

  A slight variation on the fixed viewing angle approach in that they recommend 28° to 40°.

I will focus on the human visual acuity standard – we want the television to be far enough away that we cannot see the discrete (i.e. pixel) nature of the display.

Analysis

Key Equation

Equation 1 is the key formula here.

Eq. 1

where

• N_V is the number of vertical pixels (see Figure 2a).
• AR is the aspect ratio of the screen.
• L is the television screen size measured diagonally.

Derivation

Figure 2 illustrates the key parameters used in my analysis.

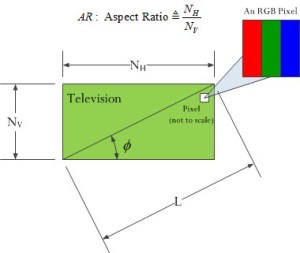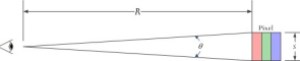Figure 2(a): Television Parameters.	Figure 2(b):Viewing Parameters.

Figure 3 shows my derivation of a formula for the minimum distance to a television based on visual acuity.

Figure 3: Derivation of Equation 1.

Results

Figure 4 shows a plot that I made of Equation 1. You can see that it is very similar to Figure 1.

Figure 4: Equation 1 Plotted Similarly to Figure 1.

This information is often presented in the form of a table. I show how to use Equation 1 to build a table of this information in Appendix A.

Conclusion

This is a quick summary of a discussion that my wife and I had this weekend. As a result of this discussion, we will be buying a 65-inch HDTV very shortly.

Appendix A: Alternative Presentation

Sometimes you will see this information presented in form, as I show in Figure 5.

Figure 5: Example of a Typical Viewing Distance Table.

Figure 6 shows my presentation of the same information computed using Equation 1.

Figure 6: My Calculation of the Info Shown in Figure 5.