Quote of the Day
Preparation is the be-all of good trial work. Everything else - felicity of expression, improvisational brilliance - is a satellite around the sun. Thorough preparation is that sun.
— Louis Nizer
Introduction
Figure 1: Typical Gage Balls.
I am still working through some examples of using gage balls for machine shop work. The following reference on Google Books has great information on using gage balls (Figure 1) in measuring the characteristics of a countersink and I will be working through the presentations there. These are good, practical applications of high-school geometry.
I will be working two examples:
- Measuring the diameter of a sharp-edged countersink
This is the simplest case and assumes that the edge is so sharp that the countersink edge touches the gage ball at a single point.
- Measuring the theoretical diameter of rounded or burred edge countersink
The theoretical countersink diameter is the diameter prior to the rounding or burring occurring.
My goal with my two gage ball blog posts (previous) is just to familiarize myself with some basic metrology.
Two Cases
Diameter of a Sharp-Edged Countersink
Equation 1 is the formula for the diameter of countersink in terms of the parameters shown in Figure 2(a).
| Eq. 1 |  |
where
- B is the diameter of the ball.
- H is the height of the ball above the surface with the countersink.
- E is the edge diameter of the countersink.
Figure 2(b) shows a construction that I use to derive Equation 1.
 Figure 2(a): Illustration from Countersink Reference. |
 Figure 2(b): Annotated Drawing of Sharp-Edged Countersink Measurement. |
Figure 3(a) shows a sharp-edged countersink example that I have contrived. Figure 3(b) shows my derivation using the Pythagorean theorem and the calculation for the example of Figure 3(a).
 Figure 3(a): Example of Measuring a Sharp-Edged Countersink. |
 Figure 3(b): Derivation and Worked Example Math. |
Diameter of a Rounded-Edge Countersink
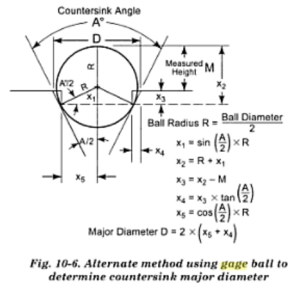
A countersink with a rounded or burred edge represents a measurement problem. If we know the diameter of the countersink taper, we can use the depth that a gage ball that fits down into the countersink to compute the theoretical (unrounded) diameter of the countersink.
Equation 2 is the formula for the diameter of countersink in terms of the parameters shown in Figure 4(a).
| Eq. 2 |  |
where
- D is the theoretical diameter of the countersink (i.e. with no rounding or burring).
Figure 4(a) shows the construction from the reference. Figure 4(b) shows a construction that I made that is just a bit less busy and I used it to derive Equation 2.
 Figure 4(a): Countersink Diameter Determination with Known Taper. |
 Figure 4(b): Annotated Drawing of Rounded-Edged Countersink Measurement. |
Figure 5(a) shows a rounded-edged countersink example that I have contrived. Figure 5(b) shows my derivation using the Pythagorean theorem and the calculation for the example of Figure 5(a).
 Figure 5(a): Example of Countersink Diameter Determination with Known Taper. |
 Figure 5(b): Derivation of Equation 2 and Example Calculation. |
Nice post, I'm working on a similar problem now. I am using gage balls to measure the radius on the edge of a thru hole and a perpendicular face. I can't stop reading your other blog posts now, awesome work!
Keep me informed of any good metrology applications you find. I am working on becoming a decent amateur machinist, and I can always use more examples.
mark
Did you realize that you used a different angle in fig 5a and 5b?
Hi Mike,
There is only one angle (A°) and it looks like it is the same in both drawings. Could you give me a bit more info?
mark
The angle in 5a is A/2=16.1939° and the angle in 5b is A=(90°-74.1954°)*2=31.6092°, so in 5b A/2=31.6092/2=15.8046°, I believe that is what Mike is saying.
You and Mike are correct. I have made the corrections. Thanks for the help!
mark
Pingback: Bore Diameter Measurement Using Gage Balls | Math Encounters Blog
Hello,
I'm having trouble reading the details of the formulas in many cases. The resolution of the figures is too low to differentiate between characters that may be similar to each other. Zooming in to the web page doesn't help.
I will try to insert a higher resolution image tonight. Sorry for the trouble.
mark
Did you click on the image to expand or just zoomed in using the browser? The images get larger and easier to read when you click directly on them.
mark
In figure 2(b), the bottom vertical segment reads (H-B) but shouldn't it be (H-(B/2))?
You are correct. Update made. Thanks.
mark
I'm looking to measure the radius on the edge of a hole thru a flat surface. Same as Will's comment from 2016 I believe. The ball diameter is known and the hole diameter is know. I want to measure the radius using the height of the ball in the hole, sitting on the radius. Do you have a solution for this?
Is this the scenario you are describing?
mark
yes, but I solved it! I can email you my excel file if you like.
Would also be interested in Riley's excel solution.
I will send Riley a note. If he does not respond, I will take a wack at it.
mark
Riley responded. He sent me the file in 2018, but it is not in my email history (I keep EVERYTHING). Anyway, here is the file. He does a nice job showing where he got the information.
Seat_radius_Calc.xlsx